* Question
What are the importance of the sampling theorem?
* Answer
The sampling theorem—often referred to as the Nyquist-Shannon Sampling Theorem—is fundamental in digital signal processing (DSP), communications, and electronics. It defines the conditions under which a continuous-time (analog) signal can be perfectly reconstructed from its samples.
Here’s a detailed breakdown of its importance:
Table of Contents
Toggle1. Foundation of Digital Signal Processing (DSP)
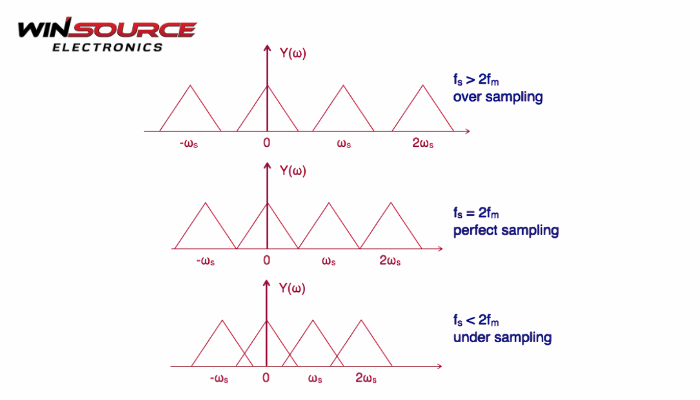
The sampling theorem ensures that analog signals can be accurately digitized without losing information. It states:
A band-limited signal with maximum frequency fmax can be completely reconstructed from its samples if it is sampled at a rate fs≥2fmax.
This rate 2fmax is known as the Nyquist rate.
Why it matters:
Ensures accurate conversion from analog to digital.
Enables real-world signals (audio, images, sensors) to be processed by computers.
2. Prevents Aliasing
Aliasing occurs when a signal is sampled below its Nyquist rate, causing different frequency components to become indistinguishable.
Why it matters:
The sampling theorem helps avoid distortion during digitization.
It ensures signal integrity and reliable data acquisition.
Encourages the use of anti-aliasing filters before sampling.
3. Supports Efficient Storage and Transmission
Knowing the minimum sampling rate necessary to capture a signal’s information:
Helps optimize data storage (audio files, images).
Reduces bandwidth requirements in communication systems.
Leads to compression algorithms that rely on sampling fundamentals (e.g., MP3, JPEG).
4. Enables Accurate Reconstruction
The theorem guarantees that under ideal conditions (infinite length and perfect sinc interpolation), the original signal can be reconstructed exactly from its samples.
Why it matters:
Supports digital-to-analog conversion (DAC) with high fidelity.
Vital for systems like:
Audio playback (CDs sample at 44.1 kHz for human hearing up to ~20 kHz)
Medical imaging (e.g., MRI)
Radar and communication systems
5. Establishes a Theoretical Framework for System Design
The sampling theorem provides a mathematical foundation for designing:
Analog-to-Digital Converters (ADCs)
Digital signal processors (DSP chips)
Signal reconstruction filters
Communication protocols and modulation schemes
Summary
Benefit | Explanation |
Accurate digitization | Converts analog to digital without information loss |
Prevents aliasing | Ensures clear, undistorted sampled signals |
Efficient resource usage | Minimizes data size and bandwidth requirements |
Enables reconstruction | Guarantees signal recovery using ideal methods |
Guides hardware design | Crucial for ADCs, DSPs, and communication systems |

COMMENTS